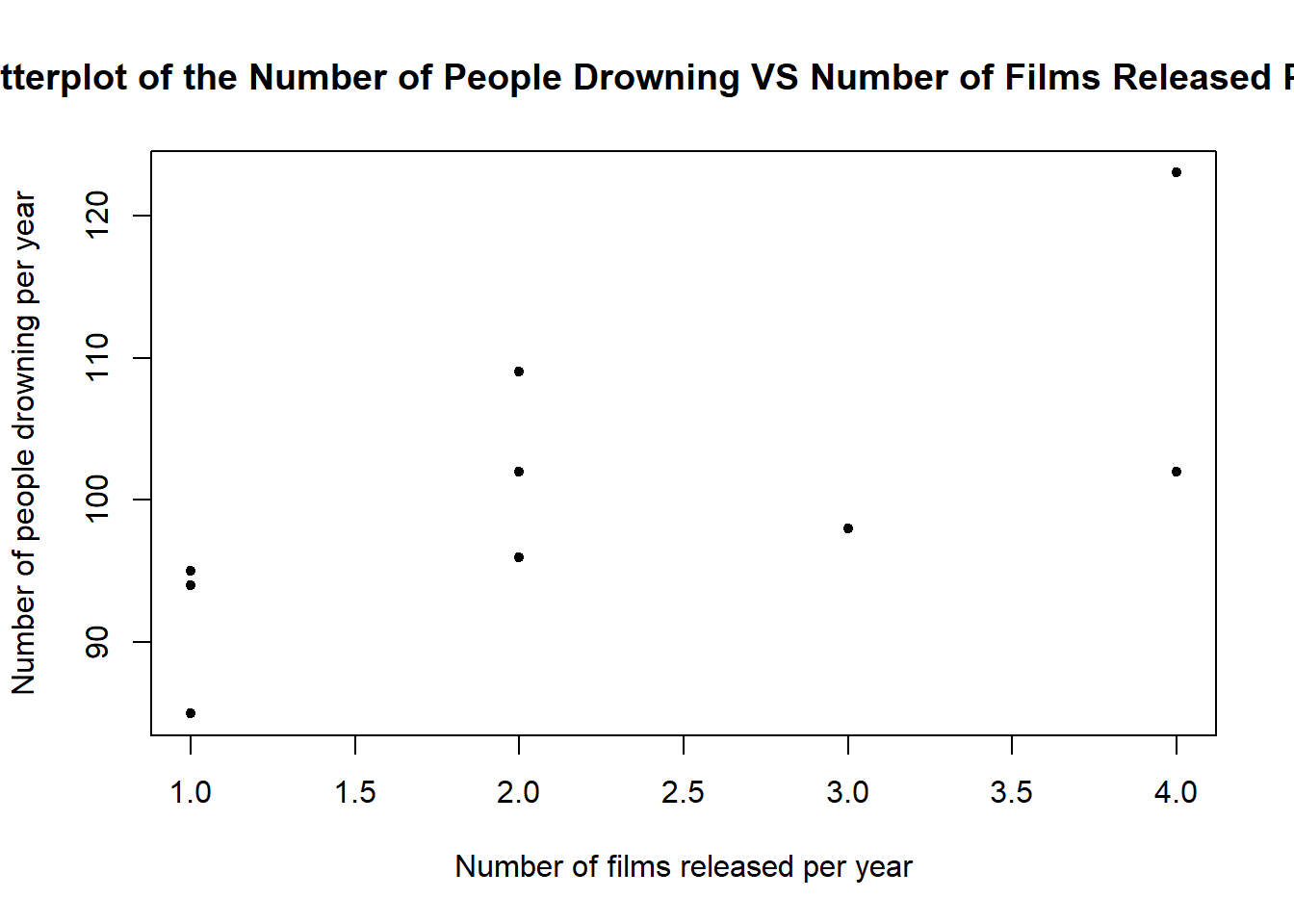
5 Example 3: Spurious correlation

Hollywood legend Nicholas Cage seems to have a problem. It appears that every time he releases a new film upon the world, many people drown by falling into pools of water. Coincidence? Or, are some of his films that bad?

Data: Cage.csv

Columns:

C1: Year Year of film releases

C2: NumFilms Number of Nicholas Cage films released that year

C3: NumDrowns Number of people who drowned falling into pools that year

To access the data, download the file Cage.csv from Moodle and make sure it is saved in an accessible file. The working directory of your RStudio Session should be set to that folder. Once this is done, read in the data using:

Cage <- read.csv("Cage.csv")

5.1 Investigating the relationship with scatterplot

To investigate the relationship between the number of films released in any year against the number of people drowning we should make a scatterplot.

TASK: Produce a scatterplot of NumDrowned against NumFilms with labels and a sensible title.

You can use plot() such as in the previous example with Grades. Or you can refer to previous weeks labs and use ggplot().

plot(NumDrowned ~ NumFilms, data = Cage, xlab = "Number of films released per year", ylab = "Number of people drowning per year", main="Scatterplot of the Number of People Drowning VS Number of Films Released Per Year", pch=20)

5.2 Further analsyis with sample correlation coefficient

cor(x=Cage$NumFilms, y=Cage$NumDrowned)

## [1] 0.6660043

QUESTION: How could we interpret this result?

The sample correlation coefficient is 0.666, indicating a weak positive linear relationship between NumDrowned and NumFilms. The sample correlation coefficient is 0.666, indicating a moderate positive linear relationship between NumDrowned and NumFilms. The sample correlation coefficient is 0.666, indicating a strong neagtive linear relationship between NumDrowned and NumFilms. The sample correlation coefficient is 0.666, indicating no significant linear relationship between NumDrowned and NumFilms.

5.3 Spurious Correlation

Does this mean that Nicolas Cage films are causing drownings? Quite obviously, the answer to this would be no. This is only correlation not causation.

In fact, this is an example of spurious correlation, where two variables that are not related to each other in any way, that is, they are independent, could be inferred as being related. The number of Nicholas Cage films released in a year is clearly not related to the number of drowning accidents in that same year, but if we just take our correlation analysis on face value, then we would think otherwise.

Reference: Spurious Correlations, Tyler Vigen